1. Az alábbi táblázat relatív
gyakoriságokat tartalmaz (%-ban megadva). Az ismérvek
függetlenségét feltétezve, írja be a hiányzó gyakoriságokat!
|
A |
B |
Össszesen |
|
|
0 |
1 |
||
|
0 |
14,4 |
|
|
|
1 |
|
|
|
|
Össszesen |
|
52 |
100 |
2. Egy felmérésben 200
megkérdezett diák közül 120 fiú és 80 lány volt. A diákok 30%-ának volt
nyelvvizsgája. A nem és a nyelvvizsga léte közötti kapcsolat erősségét kifejező
mutató Yule-féle asszociációs együttható 0 volt. Hány
lánynak van nyelvvizsgája?
3. Egy egyetem hallgatóinak
megoszlása
|
Szak |
Fiú |
Lány |
Összesen |
|
Műszaki |
2100 |
400 |
2500 |
|
Közgazdasági |
600 |
600 |
1200 |
|
Bölcsész |
300 |
1000 |
1300 |
|
Összesen |
3000 |
2000 |
5000 |
Jellemezze a nemek és a
szakok közötti kapcsolatot a Cramer-féle és Csuprov-féle asszociációs együtthatóval!
4. Elemezzük a településtípus
és a vezetékes gázzal ellátott lakások aránya közötti kapcsolatot!
|
|
Vezetékes gáz van |
Vezetékes gáz nincs |
|
Város |
81% |
19% |
|
Község |
23% |
77% |
5. Az erdők egészségi
állapota a levélvesztés alapján Magyarországon
1997-ben, 800 véletlenszerűen kiválasztott fa vizsgálata alapján:
|
Erdő típusa |
Tünetmentes |
károsodott |
elhalt |
Összesen |
|
Lombos |
263 |
330 |
15 |
608 |
|
Fenyő |
91 |
95 |
6 |
192 |
|
összesen |
354 |
425 |
21 |
800 |
Mekkora az erdő típusa és
egészségi állapota közötti kapcsolat?
6. Egy orvos feljegyezte
páciensei hajának és szemének a színét:
|
Hajszín |
Szemszín |
||
|
szürke |
Barna |
Kék |
|
|
Szőke |
1 |
4 |
18 |
|
Barna |
15 |
10 |
6 |
|
Fekete |
10 |
12 |
4 |
Van-e kapcsolat a két ismérv
között?
7. Egy vállalkozás 4
különböző (A, B, C, D) telephelyének azonos termékeiből 300 darabot vizsgáltak
meg és ezeket osztályokba sorolták. A vizsgálat eredménye a következő:
|
Minőség |
telephelyek |
összesen |
|||
|
A |
B |
C |
D |
||
|
I. osztályú |
160 |
58 |
32 |
36 |
286 |
|
II. osztályú |
6 |
5 |
26 |
77 |
114 |
|
Összesen |
166 |
63 |
58 |
113 |
400 |
Állapítsa meg, van-e
kapcsolat a termék gyártási helye és minősége között!
Megoldások:
1. A következő táblázat
jelöléseit használva, függetlenség mellett fennállnak a következő egyenlőségek:
f11/ f12= f21/ f22= f.1/ f.2; ezekből könnyen ki lehet
számolni a hiányzó adatokat.
|
A |
B |
Össszesen |
|
|
0 |
1 |
||
|
0 |
f11 |
f12 |
f1. |
|
1 |
f21 |
f22 |
f2. |
|
Össszesen |
f.1 |
f.2 |
n |
A megoldás:
|
A |
B |
Össszesen |
|
|
0 |
1 |
||
|
0 |
14,4 |
15,6 |
30 |
|
1 |
33,6 |
36,4 |
70 |
|
Össszesen |
48 |
52 |
100 |
2. Mivel az együttható értéke
0, ezért a lányok és fiúk között azonos a nyelvvizsgák aránya. Vagyis a lányok
30%-ának, 24 lánynak van nyelvvizsgája.
3. A függetlenség melletti
gyakoriság: (fi*)
|
Szak |
Fiú |
Lány |
Összesen |
|
Műszaki |
1500 |
1000 |
2500 |
|
Közgazdasági |
720 |
480 |
1200 |
|
Bölcsész |
780 |
520 |
1300 |
|
Összesen |
3000 |
2000 |
5000 |
fij-fij*
|
Szak |
Fiú |
Lány |
Összesen |
|
Műszaki |
600 |
-600 |
0 |
|
Közgazdasági |
-120 |
120 |
0 |
|
Bölcsész |
-480 |
480 |
0 |
|
Összesen |
0 |
0 |
0 |
(fij-fij*)2
|
Szak |
Fiú |
Lány |
Összesen |
|
Műszaki |
360000 |
360000 |
720000 |
|
Közgazdasági |
14400 |
14400 |
28800 |
|
Bölcsész |
230400 |
230400 |
460800 |
|
Összesen |
604800 |
604800 |
1209600 |
(fij-fij*)2/fij*
|
Szak |
Fiú |
Lány |
Összesen |
|
Műszaki |
240 |
360 |
600 |
|
Közgazdasági |
20 |
30 |
50 |
|
Bölcsész |
295 |
443 |
738 |
|
Összesen |
555 |
833 |
1388 |
A Csuprov-féle
asszociációs együttható:
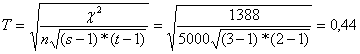
A Cramer-féle
asszociációs együttható:
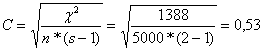
Közepes mértékű kapcsolat van
a két ismérv között.
4. Az alternatív ismérvek
közötti kapcsolat szorosságát mérő Yule-féle asszociációs
együtthatót lehet számolni:
a=Y=(f11*f22-f12*f21)/
(f11*f22+f12*f21)=(81*77-19*23)/(
81*77+19*23)=0,869 A két ismérv között
erős kapcsolat mutatható ki.
A feladatban kiszámítható a Csuprov és Cramer mutató is (meg
egyéb, nem tanult mutatók).
5. A függetlenség melletti
eloszlás: (fi*)
|
Erdő típusa |
Tünetmentes |
károsodott |
elhalt |
Összesen |
|
Lombos |
269 |
323 |
16 |
608 |
|
Fenyő |
85 |
102 |
5 |
192 |
|
összesen |
354 |
425 |
21 |
800 |
(fi-fi*)2/fi*
|
Erdő típusa |
Tünetmentes |
károsodott |
elhalt |
Összesen |
|
Lombos |
0,134 |
0,152 |
0,063 |
0,349 |
|
Fenyő |
0,424 |
0,48 |
0,2 |
1,104 |
|
összesen |
0,558 |
0,632 |
0,263 |
1,453 |
A Csuprov-féle
asszociációs együttható:
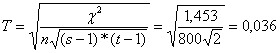
A mutató értéke csaknem
nulla, vagyis nincs kapcsolat a két ismérv között.
6. Megoldás: Csuprov-féle asszociációs együtthatót számítunk:
Az eredeti gyakoriság: (fij)
|
1 |
4 |
18 |
23 |
|
15 |
10 |
6 |
31 |
|
10 |
12 |
4 |
26 |
|
26 |
26 |
28 |
80 |
A függetlenség melletti
gyakoriság: (fij*)
|
7,48 |
7,48 |
8,05 |
23 |
|
10,08 |
10,08 |
10,85 |
31 |
|
8,45 |
8,45 |
9,10 |
26 |
|
26 |
26 |
28 |
80 |
fij-fij*
|
6,48 |
3,48 |
-9,95 |
0 |
|
-4,93 |
0,07 |
4,85 |
0 |
|
-1,55 |
-3,55 |
5,10 |
0 |
|
0 |
0 |
0 |
0 |
(fij-fij*)2
|
41,9256 |
12,0756 |
99,003 |
|
|
24,2556 |
0,0056 |
23,523 |
|
|
2,403 |
12,603 |
26,01 |
|
|
|
|
|
|
(fij-fij*)2/fij*
|
5,609 |
1,615 |
12,298 |
19,523 |
|
2,408 |
0,001 |
2,168 |
4,576 |
|
0,284 |
1,491 |
2,858 |
4,634 |
|
8,301 |
3,107 |
17,325 |
28,733 |
Csuprov-féle együttható:
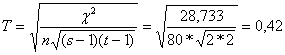
A két ismérv között van
kapcsolat (közepes).
7.
fi*
|
Minőség |
telephelyek |
összesen |
|||
|
A |
B |
C |
D |
||
|
I. osztályú |
118,7 |
45,0 |
41,5 |
80,8 |
286 |
|
II. osztályú |
47,3 |
18,0 |
16,5 |
32,2 |
114 |
|
Összesen |
166 |
63 |
58 |
113 |
400 |
(fij-fij*)2/fij*
|
Minőség |
Telephelyek |
összesen |
|||
|
A |
B |
C |
D |
||
|
I. osztályú |
14,4 |
3,7 |
2,2 |
24,8 |
45,1 |
|
II. osztályú |
36,1 |
9,4 |
5,4 |
62,3 |
113,2 |
|
Összesen |
50,5 |
13,1 |
7,6 |
87,1 |
158,3 |
Csuprov-féle együttható:
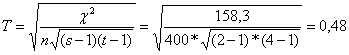
A két ismérv között van
kapcsolat (közepes).