1. példa

13 lakás ára (ezer Ft) és alapterülete (négyzetméter) közötti összefüggést vizsgálták regressziószámítással.

A részeredmények:

Lineáris regresszióhoz:

Σdxdy=57 918 000

Σd²x=495140

Σd²y=7 380 307 692

(Átlag) y=45769

(átlag) x=248

hatványkitevős regresszióhoz:

Σdlogxdlogy=1,42502

Σd²logx=1,82716

logy=4,5778

logx=2,24661

Határozzuk meg a lineáris és hatványkitevős regresszió egyenletét!

Lineáris:

β₁=57918000/495140=117

β₀=45769-117*248=16753

A regresszió egyenlete: y=16753+117x

Ha 1 négyzetméterrel növekszik a lakás alapterülete, 117 ezer forinttal növekszik az ára.

Hatványkitevős:

Ebből: β₀=669

A regresszió egyenlete: y=669*x^0,78

A regresszió szerint ha 1%-al növekszik az alapterület, 0,78%-al növekszik a lakásár.

2. példa

Megfigyelték a hektáronkénti munkaráfordítás (óra) és a hektáronkénti terméseredmény (mázsa) alakulását. Az eredmények a következők:

megfigyelés sorszáma	1	2	3	4	5	6	7	8	9	10
Munka (x)	67	72	76	76	81	81	83	85	88	91
Termés (y)	61	67	64	69	67	76	71	74	76	75

A kétváltozós regresszió eredménye:

ŷ=20,95+0,613x

SST=250

SSE=67,28

Determinációs együttható:

Adjunk becslést a 70 órás munkaráfordítású parcellák átlagára (95%-os megbízhatósági szinten)!

A reziduális szórás:

Az átlagbecslés standard hibája: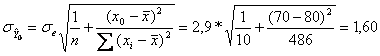

A becslés: ŷ=20,95+0,613*70=63,86

Hibahatár: 2,31*1,60=3,70

Konfidencia intervallum: 63,86±3,7 [60,16<ŷ<67,56]

A 70 órás munkaráfordítású parcellák terméseredménye 95%-os valószínűséggel a fenti intervallumba esik.

Adjunk becslést egy 70 órás munkaráfordítású parcella terméseredményére (95%-os megbízhatósági szinten)!

Standard hiba: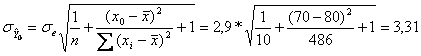

Hibahatár: 2,31*3,31=7,65

Konfidencia intervallum: 63,86±7,65 [56,21<ŷ<71,51]

Egy véletlenszerűen kiválasztott 70 órás munkaráfordítású parcella terméseredménye 95%-os valószínűséggel a fenti intervallumba esik.

3. példa

Egy taxis 15 véletlenszerűen kiválasztott fuvar alapján vizsgálta a menettávolság (x változó, km) és a menetidő (y változó, perc) közötti kapcsolatot. A következő részeredmények születtek:

Σdx*dy=1241, Σd²x=621,33, Σd²y=2952,4, x=10,67 y=26,2

Kovariancia: cov(x, y)=Σdx*dy/n=82,73 szórásnégyzet: σ²_x=41,42 σ²_y=196,83

Feladat: 1, számítsuk ki és értelmezzük a lineáris regresszió paramétereit!

2, számítsuk ki a korrelációs együtthatót és a determinációs együtthatót!

3, számítsuk ki a rugalmasságot 15 kilométeres menettávolságnál!

4, teszteljük a kapcsolat szignifikanciáját (5%)!

5, becsüljük meg 95%-os valószínűséggel a 15 kilométerhez tartozó átlagos menetidőt, valamint egy véletlenszerűen kiválasztott 15 kilométeres fuvar menetidejét!

Megoldás:

1, β₁=Σdx*dy/ Σdx²=1241/621,33=1,997

vagy: β₁=cov(x, y)/σ²_x=Σdx*dy/n /σ²_x=82,73/41,42=1,997

β₀=y- β₁*x=26,2-1,997*10,67=4,892

ŷ=4,892+2x

1 kilométerrel hosszabb fuvar átlagosan 2 perccel növeli a menetidőt. (A β₀ paramétert jelen esetben nem értelmezzük, mert ez a nulla kilométeres fuvarokhoz tartozó menetidő lenne)

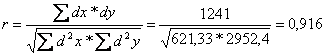
A két változó között szoros pozitív irányú kapcsolat létezik.

A determinációs együttható:

r²=0,8395 ebből az r²=(1-e²)/Σd²y összefüggés alapján e²=2952,4*(1-0,8395)=473,9

Az fuvarok távolságának az eltérése a menetidő szórásnégyzetének 83,95%-át magyarázza meg.

Ha a menettáv a 15 kilométeres szintről 1%-al nő, akkor a menetidő 0,86%-al nő.

4, A tesztelés történhet t próbával és F próbával is.

A t próba:

H₀: ß₁=0

H₁: ß₁≠0

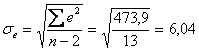
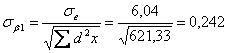
t=β₁/σ_β1=1,997/0,242=8,25

Táblázatbeli érték: szabadságfok: n-m-1=n-2=15-2=13 t_0,975=2,16

A paraméter értéke szignifikánsan különbözik nullától. A távolság és a menetidő közötti pozitív irányú kapcsolat az alapsokaságra is jellemző.

Ugyanez F próbával elvégezve: H₀: β₁=0

H₁: β₁≠0

A variancianalízis táblája:

Variancia eredete	Négyzetösszeg	Szabadságfok	Átlagos négyzetösszeg
Regresszió (SSR)	2478,5	1	2478,5
Hibatényező (SSE)	473,9	13	36,44
Együtt (SST)	2952,4	14	-

(Megjegyzés: jelen esetben csak SST volt megadva közvetlenül; az SSE-t a determinációs együttható és az SST ismeretében számoltuk ki.)

Próbafüggvény értéke:

(Megjegyzés: m a magyarázó változók száma; n a megfigyelések száma)

Táblázatbeli érték F_0,95 (1,13)= 4,67

Ennek alapján a nullhipotézis elvetendő, a lineáris regresszió (a menettávolság) az y változó szórásnégyzetét szignifikánsan magyarázza.

5, A 15 kilométeres futásteljesítmény pontbecslése: 4,892+2*15=34,895 perc

az átlagbecslés standard hibája:

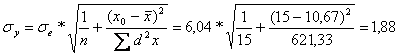
az egyedi becslés standard hibája:

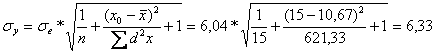
a konfidencia intervallumok:

D=2,16*1,88=4,06

D=2,16*6,33=13,67

átlagbecslés: 30,835< ŷ <38,955

A 15 kilométeres fuvarokhoz tartozó menetidők átlaga 95%-os valószínűséggel a fenti intervallumba esik.

Egyedi becslés: 21,225< Ŷ <48,565

Egy véletlenszerűen kiválasztott 15 kilométeres fuvar menetideje 95%-os valószínűséggel a fenti intervallumba esik.