Többváltozós regresszió
1.
példa
Egy strand büfése kíváncsi volt arra,
hogy milyen tényezők játszanak szerepet a sörfogyasztás alakulásában. Ezért 30
napon keresztül megfigyelte a sörfogyasztás mennyiségét (deciliter), a 15
órakor mért hőmérsékletet (˚C fok), és a strand látogatóinak a számát. Az
adatok alapján a következő többváltozós regressziós eredmények születtek:
β = [-1613 61
1,16]
σβ = [289 7,2
0,2]
|
|
1 |
0,81 |
0,78 |
|
R= |
0,81 |
1 |
0,38 |
|
|
0,78 |
0,38 |
1 |
A fenti
eredmények a következő módon is megadhatók:
|
Változó |
Átlag |
Β |
Lineáris
korrelációk Y x1 |
(X’X)-1
főátlóelemei |
|
|
Y |
857 |
-1613 |
1 |
|
0,8768 |
|
X1 |
28,7 |
61 |
0,81 |
1 |
0,00539 |
|
X2 |
620 |
1,16 |
0,78 |
0,38 |
0,0000042 |
SSE=260099
SST=3232242
Feladatok:
1,
A regressziós egyenlet felírása a paraméterek értelmezése.
2,
Mekkora a becsült forgalom egy olyan napon, amelyen a hőmérséklet 30 ˚C, a
látogatók száma 1000 fő?
3,
A paraméterek tesztelése F próbával (globális tesztelés) és t próbával
(parciális tesztelések). (α=5%)
4,
Többszörös korrelációs és determinációs együttható kiszámítása.
5,
A parciális korrelációk kiszámítása és értelmezése, összehasonlítása a teljes
korrelációkkal.
6,
A sörfogyasztás látogatók száma szerinti rugalmassága, ha az x1=28 ˚C,
és x2=1000.
Megoldás:
1, ŷ=-1613+61x1+1,16x2
A
látogatók azonos száma mellett egy fokkal magasabb hőmérséklet mellett 61
decivel több sör fogy.
Azonos
hőmérséklet mellett eggyel több látogató mellett 1,16 decivel több sör fogy.
2, ŷ=-1613+61*30+1,16*1000=1377
deciliter a becsült sörfogyasztás
3,
F próba:
H0:
β1=β2=0
H1:
βj≠0
A variancianalízis táblája:
|
Variancia eredete |
Négyzetösszeg |
Szabadságfok |
Átlagos négyzetösszeg |
|
Regresszió
(SSR) |
2972142 |
2 |
1486071 |
|
Hibatényező
(SSE) |
260099 |
27 |
9633 |
|
Együtt
(SST) |
3232242 |
29 |
- |
Próbafüggvény
értéke: ![]()
(Megjegyzés: m a magyarázó változók
száma; n a megfigyelések száma)
Táblázatbeli
érték = 3,35
Ennek
alapján a nullhipotézis elvetendő, az y változó
szórásnégyzetéből szignifikánsan nagy hányadot magyaráz a regressziófüggvény;
legalább egy szignifikáns magyarázó változó található.
(Megjegyzés:
számláló szabadságfoka: m=2; nevező szabadságfoka: n-m-1=27; ha a szignifikanciaszint 10%-os lenne, a táblázatbeli érték:
2,51; ha a szignifikanciaszint 1%-os, a táblázatbeli
érték: 5,49)
A
parciális tesztelések, t próbák:
H0:
ß1=0
H1:
ß1≠0
t=β1/σβ1=61/7,2=8,5
t=β2/σβ2=1,16/0,2=5,8
Táblázatbeli
érték: szabadságfok: n-m-1=27 t0,975=2,05
Mind
a két paraméter esetén 95%-os biztonsággal állítható, hogy értékük nem 0; a
hőmérséklet és a látogatók száma is szignifikánsan befolyásolja a sörfogyasztás
alakulását.
4.
A megadott adatokból a többszörös determinációs együttható kétféleképpen is
kiszámítható, az eltérésnégyzetösszeg felbontása
alapján és a teljes korrelációk alapján.
![]()
A
hőmérséklet és a látogatók száma együttesen a sörfogyasztás szórásnégyzetének
(ingadozásának) 92%-át magyarázza (a regressziófüggvényen
keresztül).
![]()
(Megjegyzés:
a kétféle számítás közötti minimális különbséget a kerekítés okozza: a teljes
korrelációk 2 tizedesjegyre lettek kerekítve; az
első, szórásfelbontáson alapuló számításban kerekítési hatás nem érvényesül.)
A
többszörös korrelációs együttható a többszörös determinációs együttható
négyzetgyöke: 0,959. A magyarázó változók a sörfogyasztás között nagyon erős
kapcsolat van.
5.
A parciális korrelációk:
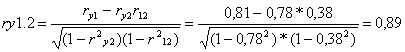
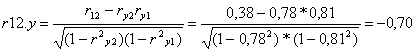
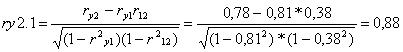
Jelentésük:
ry1.2
a hőmérséklet és a sörfogyasztás közötti kapcsolat tovább erősödött, amint a
látogatók számán keresztül érvényesülő közvetett hatást kiszűrtük. Vagyis: ha
ugyanakkora a látogatók száma, és a hőmérséklet nagyobb, akkor a sörfogyasztás
is nagyobb. (A növekedést azzal
magyarázhatjuk, hogy a nagyobb hőmérséklet a sörfogyasztást nagyobb mértékben
növeli, mint a látogatók számát.)
ry2.1
a látogatók száma és a sörfogyasztás közötti kapcsolat tovább erősödött, amint
a hőmérséklet változásán keresztüli közvetett hatást kiszűrtük. Vagyis: ha
ugyanakkor a hőmérséklet, és nagyobb a látogatók száma, akkor a sörfogyasztás
is nagyobb. (A növekedést azzal
magyarázhatjuk, hogy bár a több látogató mellett a sörfogyasztás nagyobb
mértékben növekszik, mint a hőmérséklet – bár az okozati kapcsolat a
hőmérséklet felől irányul a látogatók száma felé.)
r12.y
a hőmérséklet és a látogatók száma közötti kapcsolat előjele megfordult,
negatív lett, amint a sörfogyasztás szintjét rögzítettük. Vagyis ez azt
jelenti, hogy ugyanannyi sörfogyasztás vagy magasabb hőmérséklet és kevesebb
látogató, vagy kisebb hőmérséklet és több látogató mellett realizálódik. (Kicsit erőltetetten úgy is lehetne
fogalmazni, hogy ugyanakkora sörfogyasztás eléréséhez az alacsonyabb
hőmérsékletet lehet helyettesíteni több látogatóval, és viszont.)
6.
E(y, x1=28, x2=1000)=
![]()
Ha
adott hőmérsékleten 1000 fős szintről indulva 1%-al növekszik a látogatók
száma, akkor 0,92%-al növekszik a sörfogyasztás.
2. példa
Megfigyelték a hektáronkénti
munkaráfordítás (óra), növényvédőszer mennyisége,
valamint a hektáronkénti terméseredmény (mázsa) alakulását. Az eredmények a
következők:
x1: munka,
óra/hektár
x2: növényvédőszer, kg/hektár
y: termés, mázsa/hektár
β = [19,04 0,557
0,188]
σβ=[10,582
0,140 0,172]
korrelációs mátrix:
|
|
1 |
0,855 |
0,499 |
|
R= |
0,855 |
1 |
0,368 |
|
|
0,499 |
0,368 |
1 |
SST=250
SSE=57,5
ŷ=19,04+0,557x1+0,188x2
A megadott adatokból a
többszörös determinációs együttható kétféleképpen is kiszámítható, az eltérésnégyzetösszeg felbontása alapján és a teljes
korrelációk alapján.
![]()
A két magyarázó váltózó
együttesen a termés szórásnégyzetének (ingadozásának) 77%-át magyarázza (a regressziófüggvényen keresztül).
![]()
A parciális korrelációk:
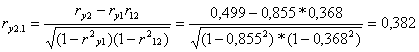
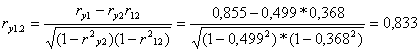
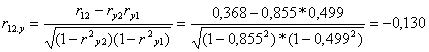
Jelentésük: A
magyarázóváltozók közül x1 van a legszorosabb kapcsolatban a
hektáronkénti terméshozammal. Azonos terméshozamot feltételezve, gyenge negatív
összefüggés van a hektáronkénti növényvédőszer
felhasználás és a munkaidő-ráfordítás között.
F próba:
H0: β1=β2=0
H1: βj≠0
A variancianalízis táblája:
|
Variancia eredete |
Négyzetösszeg |
Szabadságfok |
Átlagos négyzetösszeg |
|
Regresszió (SSR) |
192,5 |
2 |
96,25 |
|
Hibatényező (SSE) |
57,5 |
7 |
8,21 |
|
Együtt (SST) |
250 |
9 |
- |
Próbafüggvény értéke: ![]()
(Megjegyzés: m a magyarázó változók száma; n a
megfigyelések száma)
Táblázatbeli érték = 7,74
Ennek alapján a nullhipotézis elvetendő, az y változó szórásnégyzetéből
szignifikánsan nagy hányadot magyaráz a regressziófüggvény;
legalább egy szignifikáns magyarázó változó található.
Parciális próbák:
β1-re:
Próbafüggvény: t=β1/σβ1=0,557/0,14=3,98
5%-os szignifikanciaszinthez
tartozó táblabeli érték: 2,36 (szabadságfok: 10-2-1=7)
mivel a próbafüggvény értéke
nagyobb a táblabeli értéknél, ezért β1 szignifikánsan
különbözik nullától
β2-re:
Próbafüggvény: t=β2/σβ2=0,188/0,172=1,09
mivel a próbafüggvény értéke
kisebb a táblabeli értéknél, ezért β2 nem különbözik
szignifikánsan nullától
Multikollinearitás problémája: a magyarázó változók függetlensége a
paraméterek meghatározásának alapvető feltétele. Ha a magyarázó változók között
lineáris korrelációs kapcsolat van, akkor az egyes magyarázó változók hatása
nem különíthető el.
Mérőszámai, tesztelése:
R2y.12=0,770
r2y1=0,731
r2y2=0,249
x1=R2y.12-r2y2=0,770-0,249=0,521
x2=R2y.12-r2y1=0,770-0,731=0,039
M=R2y.12-(R2y.12-r2y2)-(R2y.12-r2y1)=0,770-0,521-0,039=0,210
A determinációs együttható
felbontása aszerint, hogy az egyes tényezők hogyan járulnak hozzá mértékéhez:
|
Változó |
Változók hozzájárulása az R2-hez |
|
x1 |
0,521 |
|
x2 |
0,039 |
|
x1, x2 |
0,210 |
|
Összesen |
0,770 |
Ha az egyes változók
hatásához hozzáadjuk az együttes hatást, visszakapjuk a kétváltozós
determinációs együtthatókat:
0,731=0,521+0,210
0,249=0,039+0,210
A determinációs együttható a
magyarázó változók számának nemcsökkenő függvénye.
Korrigált determinációs együtthatók:
Egy magyarázó változós
regressziónál:
![]()
Két magyarázó változós
regressziónál:
![]()
A két magyarázó változós regressziófüggvényhez tartozó korrigált determinációs együttható
nagyobb, mint az egy magyarázó változós regressziófüggvényhez
tartozó korrigált determinációs együttható. Ezen kritérium alapján a két
magyarázó változós regressziófüggvényt választjuk az
egy magyarázó változóssal szemben.
Többváltozós (négyváltozós) regresszió:
x1: munka,
óra/hektár
x2: növényvédőszer, kg/hektár
x3: csapadék, mm
y: termés, mázsa/hektár
β = [12,89 0,532
0,161 0,014]
σβ=[12,12
0,141 0,174 0,014]
korrelációs mátrix:
|
|
1 |
0,855 |
0,499 |
0,413 |
|
R= |
0,855 |
1 |
0,368 |
0,241 |
|
|
0,499 |
0,368 |
1 |
0,224 |
|
|
0,413 |
0,241 |
0,224 |
1 |
SST=250
SSE=48,9
ŷ=12,89+0,532x1+0,161x2+0,014x3
A variancianalízis
táblája:
|
Variancia eredete |
Négyzetösszeg |
Szabadságfok |
Átlagos négyzetösszeg |
|
Regresszió (SSR) |
201,1 |
3 |
67,03 |
|
Hibatényező (SSE) |
48,9 |
6 |
8,15 |
|
Együtt (SST) |
250 |
9 |
- |
Próbafüggvény értéke: ![]()
Táblázatbeli érték = 4,76
Ennek alapján a nullhipotézis elvetendő, az y változó szórásnégyzetéből szignifikánsan
nagy hányadot magyaráz a regressziófüggvény; legalább
egy szignifikáns magyarázó változó található.
determinációs együttható: ![]()
Korrigált determinációs
együttható:
![]()
A három magyarázó változós regressziófüggvényhez tartozó korrigált determinációs
együttható nagyobb, mint a két magyarázó változós regressziófüggvényhez
tartozó korrigált determinációs együttható. Ezen kritérium alapján a három
magyarázó változós regressziófüggvényt választjuk a
két magyarázó változóssal szemben.
A determinációs együttható
felbontása aszerint, hogy az egyes tényezők hogyan járulnak hozzá mértékéhez:
R2y.123=0,8044
R2y.12=0,770
R2y.13=0,776
R2y.23=0,344
x1=R2y.123-R2y.23=0,8044-0,344=0,4604
x2=R2y.123-R2y.13=0,8044-0,776=0,0284
x3=R2y.123-R2y.12=0,8044-0,770=0,0344
M= R2y.12,…,m-Σ(R2y.12,…,m-R2y.1,2,…(j-1),(j+1),…m)=0,8044-0,4604-0,0284-0,0344=0,2812
|
Változó |
Változók hozzájárulása az R2-hez |
|
x1 |
0,4604 |
|
x2 |
0,0284 |
|
x3 |
0,0344 |
|
x1, x2, x3 |
0,2812 |
|
Összesen |
0,8044 |
A három magyarázó változó
közösen magyarázza y szórásnégyzetének 28,12%-át. A munkaráfordítás önmagában
46,04%-ot, a növényvédőszer 2,84%-ot, a csapadék
3,44%-ot magyaráz.
A maradéktag normalitásának vizsgálata Kormogolov-Szmirnov
próbával:
One-Sample
Kolmogorov-Smirnov Test
|
|
reziduum |
|
|
N |
10 |
|
|
Normal Parameters(a,b) |
Mean |
,0000 |
|
|
Std. Deviation |
2,33038 |
|
Most Extreme Differences |
Absolute |
,203 |
|
|
Positive |
,203 |
|
|
Negative |
-,165 |
|
Kolmogorov-Smirnov Z |
,642 |
|
|
Asymp. Sig.
(2-tailed) |
,805 |
|
a Test distribution
is Normal.
b Calculated from data.
A megfigyelt szignifikanciaszint: p=0,805, vagyis a maradéktagok
származhatnak normális eloszlású alapsokaságból (a nullhipotézist
(=normális eloszlású alapsokaság) 80,5%-osnál nagyobb szignifikanciaszinteken
utasítanánk el).
Többváltozós (ötváltozós) regresszió:
x1: munka,
óra/hektár
x2: növényvédőszer, kg/hektár
x3: csapadék, mm
x4: műtrágya
mennyisége, kg/hektár
y: termés, mázsa/hektár
β = [-25,604 0,503
0,162 0,015 0,102]
σβ=[58,331
0,154 0,182 0,015
0,151]
korrelációs mátrix:
|
|
1 |
0,855 |
0,499 |
0,413 |
0,366 |
|
|
0,855 |
1 |
0,368 |
0,241 |
0,294 |
|
R= |
0,499 |
0,368 |
1 |
0,224 |
0,103 |
|
|
0,413 |
0,241 |
0,224 |
1 |
0,041 |
|
|
0,366 |
0,294 |
0,103 |
0,041 |
1 |
SST=250
SSE=48,9
ŷ=-25,604+0,503x1+0,162x2+0,015x3+0,102x4
A variancianalízis
táblája:
|
Variancia eredete |
Négyzetösszeg |
Szabadságfok |
Átlagos négyzetösszeg |
|
Regresszió (SSR) |
205,2 |
4 |
51,3 |
|
Hibatényező (SSE) |
44,8 |
5 |
8,96 |
|
Együtt (SST) |
250 |
9 |
- |
Próbafüggvény értéke: ![]()
Táblázatbeli érték = 5,19
Ennek alapján a nullhipotézis elvetendő, az y változó szórásnégyzetéből
szignifikánsan nagy hányadot magyaráz a regressziófüggvény;
legalább egy szignifikáns magyarázó változó található.
determinációs együttható: ![]()
Az optimális regressziófüggvény kiválasztása
valamennyi lehetséges regresszió közül a módosított determinációs együttható
alapján:
A regressziófüggvények
és a determinációs együtthatók
|
sorszám |
Regressziófüggvények |
R2 |
|
|
|
Kétváltozós |
|
|
|
1 |
ŷ =20,947+10,563x1 |
0,731 |
0,697 |
|
2 |
ŷ=55,019+9,337x2 |
0,249 |
0,155 |
|
3 |
ŷ=50,566+15,236x3 |
0,171 |
0,067 |
|
4 |
ŷ=-41,103+99,745x4 |
0,134 |
0,026 |
|
|
Háromváltozós |
|
|
|
5 |
ŷ=19,039+0,557x1+0,188x2 |
0,770 |
0,704 |
|
6 |
ŷ=13,653+0,575x1+0,016x3 |
0,776 |
0,712 |
|
7 |
ŷ=-15,256+0,587x1+0,097x4 |
0,746 |
0,673 |
|
8 |
ŷ=42,232+0,378x2-0,023x3 |
0,344 |
0,157 |
|
9 |
ŷ=-40,616+0,412x2+0,243x4 |
0,349 |
0,163 |
|
10 |
ŷ=-54,907-0,029x3+0,267x4 |
0,293 |
0,091 |
|
|
Négyváltozós |
|
|
|
11 |
ŷ=12,891+0,532x1+0,161x2+0,014x3 |
0,805 |
0,707 |
|
12 |
ŷ=-17,528+0,530x1+0,189x2+0,097x4 |
0,785 |
0,678 |
|
13 |
ŷ=-24,780+0,546x1+0,017x3+0,102x4 |
0,793 |
0,689 |
|
14 |
ŷ=-51,466+0,351x2+0,023x3+0,239x4 |
0,441 |
0,161 |
|
|
Ötváltozós |
|
|
|
15 |
ŷ=-25,604+0,503x1+0,162x2+0,015x3+0,102x4 |
0,821 |
0,678 |
Ez alapján a hatos számú regressziófüggvény az optimális: ŷ=13,653+0,575x1+0,016x3
A multikollinearitás
vizsgálata ennél a regressziónál:
R2y.13=0,776
r2y1=0,731
r2y3=0,171
x1=R2y.13-r2y3=0,776-0,171=0,605
x3=R2y.13-r2y1=0,776-0,731=0,045
M=R2y.12-(R2y.12-r2y2)-(R2y.12-r2y1)=0,776-0,605-0,045=0,126
A determinációs együttható
felbontása aszerint, hogy az egyes tényezők hogyan járulnak hozzá mértékéhez:
|
Változó |
Változók hozzájárulása az R2-hez |
|
x1 |
0,605 |
|
x3 |
0,045 |
|
x1, x3 |
0,126 |
|
Összesen |
0,776 |
A multikollinearitás
kisebb mértékű, mint amikor x1 és x2 volt a magyarázó
változó.
Minőségi ismérvek (más néven mesterséges változók vagy dummy változók) bevonása a regresszióba: eggyel kevesebb változóval
vesszük be a modellbe, mint ahány változata van az ismérvnek. Alternatív
ismérveket egy változóval, k változattal rendelkező ismérveket k-1 változóval
veszünk be.
Regressziószámítás minőségi ismérvvel:
x1: munka,
óra/hektár
x2: növényvédőszer, kg/hektár
x3: csapadék, mm
x4: műtrágya
mennyisége, kg/hektár
x5: vetőmag
minősége: értéke
y: termés, mázsa/hektár
β =[-58,227 0,519
0,200 0,003 0,191
4,173]
σβ=[32,937
0,084 0,099 0,009
0,086 1,159]
ŷ=-58,227+0,519x1+0,200x2+0,003x3+0,191x4+4,173x5
Vagyis a hektáronkénti
termésátlag (az egyes magyarázó változók hatása, miközben a többi magyarázó
változó nagysága változatlanul marad):
0,519 mázsával nagyobb, ha 1
órával nagyobb a ráfordított munkamennyiség
0,200 mázsával nagyobb, ha 1 kg-al több a növényvédőszer
0,003 mázsával nagyobb, ha 1
mm-el több a csapadék
0,191 mázsával nagyobb, ha 1 kg-al több a műtrágya mennyisége
4,173-al nagyobb az 1
osztályú vetőmagé a 2 osztályúnál
Nem mindegyik paraméter
értéke tér el szignifikánsan nullától. A t értékek:
|
paraméter |
t próbafüggvény értéke |
Megfigyelt szignifikanciaszint |
A paraméter standardizált értéke |
|
β1 |
6,18 |
0,003 |
0,724 |
|
β2 |
2,02 |
0,114 |
0,227 |
|
β3 |
0,33 |
0,735 |
0,042 |
|
β4
|
2,22 |
0,090 |
0,250 |
|
β5 |
3,60 |
0,023 |
0,417 |
A standardizált paraméterek: kiszűrik annak hatását, hogy milyen mértékegységben
vagy nagyságrendben (grammban vagy unciában, méterben vagy lábban, mázsában, kilogramban, grammban stb.) adtuk meg az adatokat; értéke
minél magasabb, annál jelentősebb a változó hozzájárulása y alakulásának
magyarázatához.
SSR=239,4
A variancianalízis
táblája:
|
Variancia eredete |
Négyzetösszeg |
Szabadságfok |
Átlagos négyzetösszeg |
|
Regresszió (SSR) |
239,4 |
5 |
47,89 |
|
Hibatényező (SSE) |
10,6 |
4 |
2,639 |
|
Együtt (SST) |
250 |
9 |
- |
Próbafüggvény értéke: ![]()
Táblázatbeli érték = 6,26
Ennek alapján a nullhipotézis elvetendő, az y változó szórásnégyzetéből
szignifikánsan nagy hányadot magyaráz a regressziófüggvény;
legalább egy szignifikáns magyarázó változó található.
determinációs együttható: ![]()
Korrigált determinációs
együttható:
![]()
A korrigált determinációs
együttható nagyobb, mint a korábban vizsgált regressziók bármelyikében.
Elhagyva az x3 változót, amelynek értéke nem bizonyult
szignifikánsan különbözőnek nullánál, a következő regressziót kapjuk:
ŷ=-57,983+0,525x1+0,207x2+0,193x4+4,330x5
A t értékek:
|
paraméter |
t próbafüggvény értéke |
Megfigyelt szignifikanciaszint |
A paraméter standardizált értéke |
|
β1 |
7,00 |
0,001 |
0,732 |
|
β2 |
2,33 |
0,067 |
0,234 |
|
β4
|
2,49 |
0,055 |
0,253 |
|
β5 |
4,43 |
0,007 |
0,433 |
A megfigyelt szignifikanciaszintek minden esetben elég kicsik.
(Legnagyobb a β2-nél, ott 6,7%-os szignifikanciaszint
alatt elfogadnánk a nullhipotézist, vagyis hogy a
paraméter értéke nullával egyenlő lehet az alapsokaságban.)