


Next: About this document ...
Gyakorló feladatlap a ,,Komplex számok'' témakörből
1999. október 6.
- Ábrázold a komplex számsíkon azokat a halmazokat, amelyeket az alábbi
feltételnek megfelelő
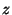 komplex számok alkotnak:
komplex számok alkotnak:
- Legyen
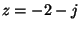 ,
, 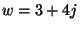 . Számítsd ki az alábbi kifejezések értékét!
. Számítsd ki az alábbi kifejezések értékét!
- Tekintsük az alábbi komplex számokat:
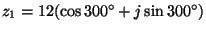 ,
, 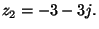
Add meg azokat az 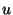 ,
, 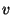 és
és 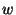 komplex számokat algebrai és
trigonometrikus alakban is, amelyekre
komplex számokat algebrai és
trigonometrikus alakban is, amelyekre
- Oldd meg az alábbi egyenleteket a komplex számok között! Az eredményt
algebrai és trigonometrikus alakban is add meg és ábrázold a komplex
számsíkon!
- Határozd meg azt a
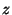 komplex számot, melyre
komplex számot, melyre
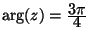 és
és
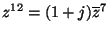 ?
?
- Mely komplex számokra egyenértékű
- Hány megoldása van az alábbi egyenleteknek a valós, illetve a komplex számok
között?
Horváth Zoltán
1999-10-06
![]() ,
, ![]() és
és ![]() komplex számokat algebrai és
trigonometrikus alakban is, amelyekre
komplex számokat algebrai és
trigonometrikus alakban is, amelyekre
![]() ,
, ![]() és
és ![]() komplex számokat algebrai és
trigonometrikus alakban is, amelyekre
komplex számokat algebrai és
trigonometrikus alakban is, amelyekre