![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

A differenciálegyenletek fogalma és osztályozása
Differenciálegyenletnek azokat az egyenleteket nevezzük, amelyekben az ismeretlen egy egy- vagy többváltozós függvény és az egyenlet tartalmazza ezen függvény valamilyen deriváltját is. Például az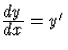 ,
,
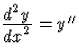 , stb., továbbá a
parciális deriváltakra az alsó indexes jelölésmód: ennek
példáját (5)-ben látjuk:
, stb., továbbá a
parciális deriváltakra az alsó indexes jelölésmód: ennek
példáját (5)-ben látjuk: 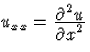 (így (4) és (5) ugyanazt a
differenciálegyenletet jelenti).
(így (4) és (5) ugyanazt a
differenciálegyenletet jelenti).
Az ismeretlen függvény deriváltjai közül az előforduló legmagasabb rendű derivált rendjét a differenciálegyenlet rendjB<>enek nevezzük. Így (1) elsőrendű, (3) harmadrendű, (2), (4) és (5) másodrendű.
Ha az ismeretlen függvény egyváltozós, akkor a differenciálegyenletet közönséges differenciálegyenletnek, míg ha többváltozós (így a deriváltja(i) parciális deriváltak), akkor parciális differenciálegyenletnek nevezzük. Eszerint (1), (2), (3) közönséges, míg (4) parciális.
A differenciálegyenletek között a lineáris differenciálegyenletek fontos szerepet töltenek be, mert megoldhatóságuk eldöntése és a megoldásuk felírása alaposan tanulmányozott és viszonylag könnyen elvégezhető. Lineárisnak nevezünk egy differenciálegyenletet, ha benne az ismeretlen függvény és annak deriváltjai nem fordulnak elő sem egy szorzat (vagy hányados) mindkét tényezőjében, sem elsőfokú polinomtól különböző függvény belső függvényeként.Ellenkező esetben nemlineáris differenciálegyenletről beszélünk. Így (1), (4), (5) lineáris, míg (2), (3) nemlineáris.
![[*]](nyil_elore.gif)
Készült a SZIF-MML-rendszer felhasználásával