![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

Az 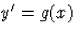 eset
eset
Itt tehát f(x,y)=g(x), azaz az egyenlet jobb oldala független az
ismeretlen y függvénytől. Ekkor a megoldást g primitív függvényei
szolgáltatják:
![]()
Ha még adott az y(x0)=y0 kezdeti feltétel is, akkor c-t úgy kell megválasztanunk, hogy ez az egyenlőség fennálljon, azaz G(x0)+c=y0 legyen, ahonnan
c=y0-G(x0),
így az egyértelmű megoldás azy(x)=y0+G(x)-G(x0)
alakot ölti.Mivel G a g függvény egy primitív függvénye és feltevésünk szerint g folytonos, ezért a Newton-Leibniz-formula miatt

 |
(34) |
![[*]](nyil_elore.gif)
Készült a SZIF-MML-rendszer felhasználásával