![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)
 |
Elsőrendű, közönséges differenciálegyenletek néhány osztályának
megoldása
Tekintsük az
differenciálegyenletet.
Láttuk az előzőekben, hogy a differenciálegyenlet jobb oldalának, az f=f(x,y)
kétváltozós függvénynek az ismeretében gyakran eldönthető, hogy a
differenciálegyenletnek van-e megoldása. Azonban a fenti tételek arról nem adnak
információt, hogy a megoldás hogyan írható fel. Ebben az
alfejezetben olyan speciális f-eket vizsgálunk meg, amikor a
megoldást elő tudjuk állítani valamilyen formában.
Általában a megoldást nem kaphatjuk meg egy zárt képlet alakjában,
például az
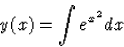
függvények a
határozatlan integrál definíciója miatt kielégítik az
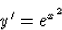
egyenletet, azonban bizonyított, hogy ezek az y(x) függvény
ek nem írhatók fel csak az elemi függvények (azaz a hatvány-,
exponenciális-, trigonometrikus függvények, ezek inverzei)
felhasználásával véges sok művelet (összeadás, szorzás,
osztás, függvénykompozíció) segítségével, röviden véges képlettel.
Sőt, még az sem elegendő differenciálegyenletek megoldásainak
véges képlettel való felírhatóságához, hogy megengedjük
még az eddigi értelemben véges képletű függvények primitív függvényeinek
(így pl. az előző differenciálegyenlet megoldásának) a szerepeltetését a
képletekben: az
is bizonyított, hogy az
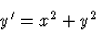
egyenletnek még így sem
adható meg
véges képlettel a megoldása (de megoldása van). Ezért -
kicsit tréfásan szólva - örülnünk kell, ha egy differenciálegyenletből el
tudjuk tüntetni a deriváltakat és az integráljeleket. Amikor nem
sikerül, akkor valamilyen közelítő módszerre (pl. a megoldás
Taylor-polinomjainak előállítására) van szükségünk.
Ezzel a kérdéssel majd egy későbbi fejezetben foglalkozunk.
Most tehát az
differenciálegyenletekkel foglalkozunk, speciális f-ek mellett.
A továbbiakban feltételezzük, hogy az egyenletnek létezik
megoldása, ami pl. f mint kétváltozós függvény folytonossága mellett
állítható.
|
![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

![]()
![]()
![]()
![[*]](nyil_elore.gif)