![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

A megoldás létezéséről és egyértelműségéről
Mielőtt nekilátnánk az előző szakaszban kitűzött feladatok (kezdetiérték-feladatok és peremérték-feladatok) megoldásához, felvetődik a kérdés, hogy egyáltalán megoldható-e a vizsgált feladat és ha igen, akkor hány megoldása van. Ezen kérdések megválaszolása nemcsak elméleti, de gyakorlati szempontból is érdekes lehet. Gondoljunk csak bele a következőkbe. Tegyük fel, hogy tudjuk: a tekintett feladatnak megfelelő fizikai problémának egyféle megoldása, lefolyása van. Ha kiderül a matematikai feladatról, hogy annak nincs megoldása, vagy esetleg több is van, akkor ez azt jelenti, hogy a matematikai modell felállítása nem volt jó: az első esetben talán túl sok, a másodikban talán túl kevés feltételt vettünk figyelembe a feladat felállításakor, így a fizikai jelenség leírását újra kell gondolnunk.
Ezek után vizsgáljuk meg az előző szakaszban megfogalmazott feladatokat a megoldás létezése és ennek megléte esetén egyértelműsége szempontjából. (Ezt a kérdéskört a , ,megoldás egzisztenciája és unicitása'' elnevezéssel szokták illetni.)
Számtalan különféle eset előfordulhat, amint azt az alábbi példák mutatják.
- 1.
- nincs megoldása a differenciálegyenletnek:
ahol d az úgynevezett Dirichlet-függvény: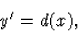
(29)
Ennek a differenciálegyenletnek nincsen megoldása, mert a Darboux-féle középérték-tétel szerint ha egy függvény deriváltja felvesz két értéket, akkor e két érték között minden más valós számot is felvesz; márpedig ha lenne megoldása (38)-nak, akkor deriváltja bármely intervallumon csak 0-t és 1-et venne fel és közöttük semmit.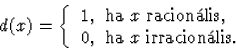
- 2.
- nincs megoldása a kezdetiérték-feladatnak, de a hozzá tartozó differenciálegyenletnek van:
ahol sign az előjelfüggvény: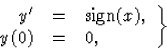
(30)
E kezdetiérték-feladatnak nincs megoldása, hiszen az előbb említett Darboux-tétel miatt az x0=0 pont környezetében nincs olyan y függvény, melynek a sign függvény lenne a deriváltja. Az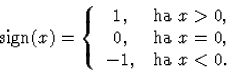
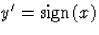 differenciálegyenletnek viszont van megoldása, pl. az y(x)=x+c
alakú függvények (ahol c tetszőleges valós szám) mind megoldásai a
differenciálegyenletnek viszont van megoldása, pl. az y(x)=x+c
alakú függvények (ahol c tetszőleges valós szám) mind megoldásai a
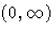 intervallumon, amint erről visszahelyettesítéssel
könnyen meggyőződhetünk.
intervallumon, amint erről visszahelyettesítéssel
könnyen meggyőződhetünk.
- 3.
- a kezdetiérték-feladatnak egy megoldása van:
Az analízisből tudjuk, hogy ha egy függvény deriváltja egy intervallumon azonosan 0, akkor a függvény ezen az intervallumon állandó. A kezdeti feltétel miatt ez az állandó csak a 0 lehet. Így bebizonyítottuk, hogy (40)-nek csak az azonosan 0 függvény a megoldása.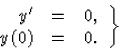
(31) - 4.
- a kezdetiérték-feladatnak végtelen sok megoldása van:
Könnyen meggyőződhetünk róla, hogy az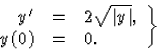
(32)
alakban írható függvények tetszőleges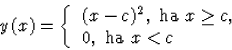
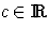 esetén megoldását
adják a differenciálegyenletnek és
esetén megoldását
adják a differenciálegyenletnek és
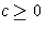 esetén még a kezdeti feltételt is kielégítik.
esetén még a kezdeti feltételt is kielégítik.
- 5.
- a peremérték-feladatnak nincs megoldása, de a hozzá tartozó
differenciálegyenletnek van:
A 3. fejezetben be fogjuk látni, hogy a differenciálegyenlet összes megoldása felírható az
alakban. y(0)=1-ből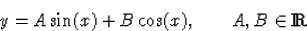
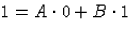 , azaz B=1,
, azaz B=1, 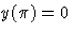 -ból
-ból
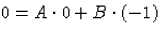 , azaz B=0 következik, így a perem érték
feladatnak nincs megoldása.
, azaz B=0 következik, így a perem érték
feladatnak nincs megoldása.
Ugyanez a helyzet akkor is, ha a peremfeltételt kicseréljük az
másodfajú feltételre.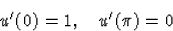
- 6.
- a perem érték feladatnak egy megoldása van:
Mivel
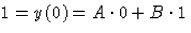 , ezért B=1; továbbá
, ezért B=1; továbbá
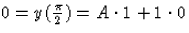 , tehát A=0. Így az egyetlen
megoldás:
, tehát A=0. Így az egyetlen
megoldás: 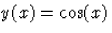 .
. - 7.
- a perem érték feladatnak végtelen sok megoldása van:
Könnyű belátni, hogy az
alakú függvények megoldásai a feladatnak, ahol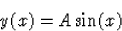
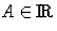 tetszőleges.
tetszőleges.
A most következő két, bizonyítás nélkül![[*]](foot_motif.gif) közölt tétel elégséges feltételt nyújt elsőrendű kezdetiérték-feladatok
megoldásának létezésére, illetve a megoldás egyértelműségére.
közölt tétel elégséges feltételt nyújt elsőrendű kezdetiérték-feladatok
megoldásának létezésére, illetve a megoldás egyértelműségére.
Tétel. (egzisztencia-tétel) Tegyük fel, hogy az f kétváltozós függvény folytonos a
| |
(33) |
Ekkor az (36), (37) kezdetiérték-feladatnak létezik megoldása. Ez
értelmezve van az ![]() intervallumon, ahol
intervallumon, ahol ![]() az
a és a b/K számok közül a kisebbik.
az
a és a b/K számok közül a kisebbik.
Megjegyzés. A tétel feltétele, f folytonossága szükséges is a megoldás létezéséhez abban az értelemben, hogy lehet mutatni példát: e feltétel nem teljesül és a kezdetiérték-feladatnak nincs megoldása; ilyen az előbb tekintett 2. példa feladata is.
A megoldás egyértelműségéről szóló tétel kimondása előtt hasznos bevezetni az alábbi definíciót.
Definíció. Legyen az f
kétváltozós függvény értelmezett a ![]() halmazon. Azt mondjuk,
hogy f-re H-n a második változójában teljesül a
Lipschitz-feltétel, ha létezik olyan L valós szám, mellyel tetszőleges
halmazon. Azt mondjuk,
hogy f-re H-n a második változójában teljesül a
Lipschitz-feltétel, ha létezik olyan L valós szám, mellyel tetszőleges
![]() esetén érvényes az
esetén érvényes az
![]()
Megjegyzés. A Lipschitz-feltétel lényegében annak a
feltétele, hogy f ne nőjön túl gyorsan a második
változójában. Ezt jobban megvilágítja az az (itt bizonyításra nem kerülő)
állítás, miszerint ha ![]() létezik és folytonos H-n,
akkor f-re H-n a második változóban pontosan akkor teljesül a
Lipschitz-feltétel,
ha korlátos H-n, azaz létezik
létezik és folytonos H-n,
akkor f-re H-n a második változóban pontosan akkor teljesül a
Lipschitz-feltétel,
ha korlátos H-n, azaz létezik ![]() ,mellyel
,mellyel 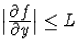 H minden
pontjában.
H minden
pontjában.
Tétel. (unicitási tétel) Ha f folytonos és a (42) alatti T halmazon teljesíti a Lipschitz-féle feltételt, akkor a fent definiált intervallumon a megoldás egyértelmű.
Megjegyzés.
Bizonyos értelemben az unicitási tétel feltétel is szükséges: a
4. példában közölt kezdetiérték-feladatnak végtelen sok megoldása van és rá
nem is teljesülnek az unicitási tétel feltételei: ugyan a
hozzátartozó ![]() függvény folytonos, de nem teljesíti a
Lipschitz-feltételt, hiszen pl. y1=0, y2>0 esetén T-n
függvény folytonos, de nem teljesíti a
Lipschitz-feltételt, hiszen pl. y1=0, y2>0 esetén T-n
![]()
Hasonló tételek mondhatók ki másodrendű differenciálegyenletekhez kapcsolódó kezdetiérték-feladatokra is: az f jobb oldal folytonossága elegendő a megoldás létezéséhez, illetve ha f folytonos, továbbá f második és harmadik változójában teljesíti a Lipschitz-féle feltételt, akkor a kezdetiérték-feladat megoldása egyértelmű.
Peremérték-feladatok esetén a megfelelő tételek jóval bonyolultabbak. Ezt lehet sejteni a tételek előtti példákból is: pl. nem elég csak az f függvény folytonosságát vizsgálni a megoldás létezéséhez, hiszen a fenti 5-7. példákban f végig ugyanaz, folytonos, de egyszer van megoldása, máskor nincs.
4-1. kidolgozott feladat.
Vizsgáljuk az
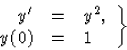
Megoldás:
Mivel f(x,y)=y2 folytonos, ezért a kezdetiérték-feladatnak biztosan van megoldása.
Határozzunk meg egy olyan intervallumot, ahol a megoldás értelmezett!
Ehhez válasszuk meg az egzisztencia-tételben szereplő T tartományt
pl. az 5=2, b=2-nek megfelelő módon, azaz T a (-5,-1), (5,-1),
(5,3), (-5,3) csúcspontokkal rendelkező négyzet. Könnyű látni,
hogy T-n ![]() , ezért az 5 és 2/9 számok
közül a kisebbik, azaz 2/9. Így a megoldás(ok) értelmezve van(nak)
a (-2/9,2/9) intervallumon.
, ezért az 5 és 2/9 számok
közül a kisebbik, azaz 2/9. Így a megoldás(ok) értelmezve van(nak)
a (-2/9,2/9) intervallumon.
Hány megoldás van? Mivel 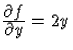 korlátos
T-n, ezért teljesül rá a Lipschitz-feltétel. Így a fenti
intervallumon a megoldás egyértelmű.
korlátos
T-n, ezért teljesül rá a Lipschitz-feltétel. Így a fenti
intervallumon a megoldás egyértelmű.
![[*]](nyil_elore.gif)
Készült a SZIF-MML-rendszer felhasználásával