![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

Differenciálegyenletekkel kapcsolatos feladatok kitűzése
Az előző pontban láthattuk, hogy egy fizikai problémához tartozó differenciálegyenlet mellé természetes módon társulhatnak az ismeretlen függvény re vonatkozó egyéb feltételek.Így például a pontszerű test hőmérsékletét leíró differenciálegyenlet mellé felírhatjuk a testnek a megfigyelés kezdetekor mért hőmérsékletét, az RLC-áramkör töltését leíró (15) differenciálegyenlethez a kezdeti töltést és áramerősséget. Ezek mindegyike olyan feltétel az ismeretlen függvényre nézve, amely egy adott pontban megadja az értékét (ezt olyan fizikai feladatoknál figyeltük meg, ahol a megfelelő differenciálegyenlet elsőrendű), vagy egy pontjában az ismeretlen függvénynek és deriváltjának is az értékét (ez bizonyos másodrendű differenciálegyenleteknek megfelelő feladatok esetén fordul elő). Ezért (is) érdemes bevezetni a differenciálegyenletekhez tartozó kezdetiérték-feladat fogalmát.
Definíció. Elsőrendű (közönséges) differenciálegyenletekre vonatkozó kezdetiérték-feladatnak az
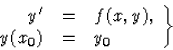 |
(24) |
Definíció. Másodrendű (közönséges) differenciálegyenletekre vonatkozó kezdetiérték-feladatnak az
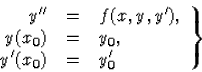 |
(25) |
Bizonyos közönséges differenciálegyenletekhez más típusú mellékfeltételek társulnak. Ilyen például a stacionárius hővezetés feladata, ahol a természetes mellékfeltétel az volt, hogy a rúd két végpontján adtunk feltételeket az ismeretlen u függvényre (lásd a 10. oldalt). Ilyen feltétel gyakran fordul elő másodrendű differenciálegyenletekkel kapcsolatban, így érdemes bevezetni a következő definíciókat.
Definíció. Másodrendű (közönséges) differenciálegyenletekre vonatkozó elsőfajú peremérték feladatnak az
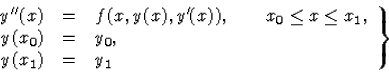 |
(26) |
Definíció. Másodrendű (közönséges) differenciálegyenletekre vonatkozó másodfajú peremérték feladatnak az
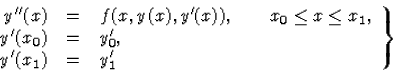 |
(27) |
A parciális differenciálegyenletekhez tartozó mellékfeltételek lényegében az előbb definiált kezdeti és peremfeltételek ötvözetei. Mi most csak az egy dimenziós hővezetési egyenlethez kapcsolódó első- és másodfajú peremfeltételekkel rendelkező vegyes feladatok definícióját adjuk meg.
Definíció. A hővezetési differenciálegyenlethez tartozó vegyes kitűzésű, elsőfajú peremfeltételekkel rendelkező feladatnak a
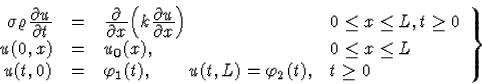
Másodfajú peremfeltételekkel rendelkező, vegyes kitűzésű feladatnak egy ugyanilyen feladatot nevezünk, csak a feltételek közül az utolsó sor kicserélendő a
![]()
Miután kitűztük a feladatainkat, fogalmazzuk meg pontosan, hogy mit értünk differenciálegyenletek, illetve az előbb definiált kezdeti és peremérték feladatok megoldásán.
Definíció. Azt mondjuk, hogy az y=y(x) függvény megoldása az
| |
(28) |
Megjegyezzük, hogy a definíció magába foglalja az y függvény deriválhatóságát és azt, hogy minden
![]() -ra (x,y(x)) eleme f értelmezési
tartományának.
-ra (x,y(x)) eleme f értelmezési
tartományának.
Definíció. Azt mondjuk, hogy y kielégíti a
![[*]](foot_motif.gif) és teljesíti az
(37) kezdeti feltételt.
és teljesíti az
(37) kezdeti feltételt.
Gyakran találkozunk olyan differenciálegyenletekkel, amelyekhez találunk egy paraméter(eke)t tartalmazó képletet, mely rendelkezik azzal a tulajdonsággal, hogy a paraméter(ek) adott intervallum(ok)ból való választásai esetén előálló formulák a differenciálegyenlet összes megoldását megadják. Ebben az esetben azt mondjuk, hogy a paramétereket tartalmazó képlet a differenciálegyenlet általános megoldása.
Így például az a kijelentés, miszerint az ![]() differenciálegyenletnek
az általános megoldása
differenciálegyenletnek
az általános megoldása ![]() az azt jelenti, hogy
minden egyes c valós szám esetén az y=cex függvény megoldása a differenciálegyenlet
nek és más megoldása nincs is, mint azok a függvények, melyek valamilyen
c valós számmal cex alakra hozhatók.
az azt jelenti, hogy
minden egyes c valós szám esetén az y=cex függvény megoldása a differenciálegyenlet
nek és más megoldása nincs is, mint azok a függvények, melyek valamilyen
c valós számmal cex alakra hozhatók.
Amikor a differenciálegyenlet csak egy bizonyos megoldásáról beszélünk, akkor azt - az általános megoldástól megkülönböztetendő - a differenciálegyenlet partikuláris megoldásának nevezzük.
Teljesen hasonlóan mondhatók ki az
![]()
![[*]](nyil_elore.gif)
Készült a SZIF-MML-rendszer felhasználásával