![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

Az 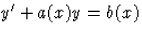 eset
eset
(Ezek az elsőrendű lineáris egyenletek.)
Megemlítjük, hogy az egyenletet azért hívják lineárisnak, mert az ismeretlen y függvény csak az első hatványon szerepel f(x,y)-ban (ami most -a(x)y+b(x)).
Az egyenletet az állandó variálásának módszerével oldjuk meg.
Először oldjuk meg a lineáris egyenletünknek megfelelő
![]()
ahol A(x) a a(x) függvény egy primitív függvénye és c tetszőleges valós szám. Mivel a jobb oldal mindig pozitív (lévén egy valós szám exponenciális függvénye) és yh folytonos, ezért yh=+ece-A(x), vagy yh=-ece-A(x). Továbbá, az első egyenlethez yh-val való osztással jutottunk, így ellenőrizni kell, vajon yh=0 megoldása-e a (homogén) differenciálegyenletnek. Könnyen láthatjuk, hogy igen. Így a homogén egyenletnek az
![]()
| |
(40) |
| y(x)=C(x)e-A(x) | (41) |
Megjegyezzük, hogy nem zártunk ki egyetlen függvényt sem azzal, hogy az egyenlet megoldását (51) alakjában keressük: tetszőleges y(x) függvényhez van olyan C(x) függvény amellyel y(x)=C(x)e-A(x), ugyanis a C(x)=y(x)eA(x) függvény megfelelő.
Helyettesítsük be az (51) alatti y(x) függvényt az eredeti egyenletbe, majd oldjuk meg C(x)-re! (A függvények argumentumában szereplő x-eket a könnyebb olvashatóság kedvéért a második egyenlettől kezdve elhagyjuk.)
ahonnan
![]()
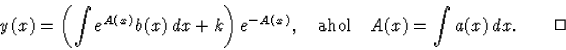 |
(42) |
Most lássunk néhány kidolgozott feladatot.
4-1. kidolgozott feladat.
Oldjuk meg az
![]()
Megoldás: Az egyenlet lineáris. Először oldjuk meg a megfelelő homogén lineáris differenciálegyenletet!
![]()
yh=Ce-6x.
, ,Variáljuk'' a konstanst, azaz keressük az inhomogén differenciálegyenlet megoldását| y=C(x)e-6x | (43) |
Visszahelyettesítve ezt az alakot a differenciálegyenletbe kapjuk
![]()
Ezt megoldva a
![]()
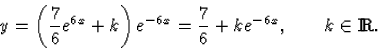
4-2. kidolgozott feladat.
Adjuk meg az
![]()
a)
b) 0-ban 1 a határértéke!
Megoldás: A megfelelő homogén differenciálegyenletet megoldva
Ezért a megoldást az
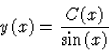
Ezért a differenciálegyenlet megoldása:
| |
(44) |
Az a) kérdést megválaszolandó olyan k számot kell keresni, amelyre
![]()
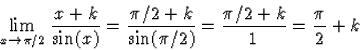
A b) kérdés megválaszolásánál óvatosnak kell lennünk, mert 0 nem eleme a (54) alatti y függvények értelmezési tartományának. Azonban 0-nak a bal és a jobb oldali környezetében értelmezve vannak. Próbáljunk olyan k értéket találni, amellyel a fenti y bal és jobb oldali határértéke egyaránt 1.
Mivel a nevező határértéke 0, ezért a tört határértéke csak akkor lehet egy véges szám, ha a számlálónak is 0 a határértéke. (De ez nem elégséges hozzá.) Így k csak 0 lehet. Szerencsénkre a k=0-hoz tartozó
| |
(45) |
Megjegyzés. A (55) alatti y függvény nincs értelmezve 0-ban,
de határértéke létezik, ez 1. Így ha értelmezzük y-t a 0
pontban az y(0):=1 egyenlőséggel, akkor folytonos függvényt kapunk.
Megmutatható, hogy az így előálló
függvény még differenciálható is a 0-ban és ![]() . Ezért y
kielégíti a differenciálegyenletet még ebben a pontban is (hiszen behelyettesítve
. Ezért y
kielégíti a differenciálegyenletet még ebben a pontban is (hiszen behelyettesítve
![]() -t a differenciálegyenletbe azonosságot kapunk:
-t a differenciálegyenletbe azonosságot kapunk:
![]() valóban).
valóban).
4-3. kidolgozott feladat.
Adjuk meg az
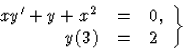
Megoldás: Alkalmazzuk most a differenciálegyenlet megoldásának megkeresésére a (52) alatti formulát! Ehhez először a differenciálegyenletet kell a megfelelő alakra hozni.
![]()
![]()
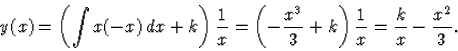
Behelyettesítve a kezdeti értéket
![]()
![]()
4-4. kidolgozott feladat.
Oldjuk meg az
![]()
Megoldás: A megfelelő homogén egyenletet megoldva
A konstanst variálva y-t az
![]()
így ![]() .Ezért a differenciálegyenlet megoldása:
.Ezért a differenciálegyenlet megoldása:
![]()
4-5. kidolgozott feladat.
Oldjuk meg az
![]()
Megoldás: Először adjuk meg a megfelelő homogén egyenlet megoldását!
Keressük ezért az inhomogén egyenlet megoldását
y=C(x)x2
alakban! Helyettesítsük ezt be a differenciálegyenletbe és oldjuk meg az előálló egyenletet C-re!Ezért a differenciálegyenlet megoldása:
![]()
![[*]](nyil_elore.gif)
Készült a SZIF-MML-rendszer felhasználásával