![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

Egzakt differenciálegyenletek
Mielőtt rátérnénk az egzakt differenciálegyenletek tárgyalására, érdemes felidéznünk a kétváltozós függvények felhasználásával készített egyváltozós függvények deriválására szolgáló formulát, a láncszabályt.![[*]](foot_motif.gif)
Állítás. Ha az F=F(x1,x2) kétváltozós függvény mindkét változója szerint deriválható, továbbá az u=u(x) és v=v(x) egyváltozós függvények deriválhatóak, akkor a
![]()
| |
(46) |
Megjegyzés. Ebben az alfejezetben kétváltozós függvények változóira az x1, x2 jeleket használjuk az eddigi x, y helyett, hogy az y betű kettős jelentése (egyrészt változó, másrészt függvény) ne okozzon kezdetben zavart. Később, a feladatok során is visszatérünk a megszokottabb x, y változókra.
Ismétlésképpen mutatunk néhány példát a láncszabály alkalmazására.
1. példa. F(x1,x2)=x1+x2. Ekkor ![]() .Továbbá
.Továbbá ![]() ,
, ![]() , így
, így ![]() . (Azaz
visszakaptuk az összeg deriválási szabályát.)
. (Azaz
visszakaptuk az összeg deriválási szabályát.)
2. példa. F(x1,x2)=x1x2. Ekkor ![]() .Kiszámítva a parciális deriváltakat:
.Kiszámítva a parciális deriváltakat:
![]()
azaz visszakaptuk az ún. logaritmikus deriválás szabályát.
| |
(47) |
Írjuk fel a jobb oldalon szereplő f függvényt az alábbi alakban:
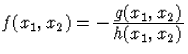 . Ez az átalakítás
persze nagyon sokféleképpen megtehető, mi ezek közül kiválasztunk egyet. Azzal
majd később foglalkozunk, hogy hogyan célszerű ezt megtenni.
. Ez az átalakítás
persze nagyon sokféleképpen megtehető, mi ezek közül kiválasztunk egyet. Azzal
majd később foglalkozunk, hogy hogyan célszerű ezt megtenni.
Így egyenletünk az
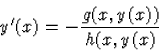
| |
(48) |
(58), és így (57) megoldásának alapötlete
a következő: vegyük észre, hogy (56) jobb és (58)
bal oldala elég nagy hasonlóságot mutat. Valóban, ha a
![]() függvényre alkalmazzuk a (56) alatti láncszabályt
(u(x)=x, v(x)=y(x) választással), akkor a
függvényre alkalmazzuk a (56) alatti láncszabályt
(u(x)=x, v(x)=y(x) választással), akkor a
| |
(49) |
| |
(50) |
![]()
| |
(51) |
Ezzel bebizonyítottuk az alábbi állítást.
Állítás. Ha a (58) egyenlethez létezik olyan F függvény melyre (60) és (61) teljesül, akkor az y=y(x) függvény pontosan akkor megoldása a (58), és így a (57) differenciálegyenletnek, ha y deriválható és valamilyen valós c állandóval kielégíti a (63) egyenletet.
Így differenciálegyenletek egy fontos osztályára fel tudjuk írni a megoldást, (még akkor is, ha (63) csak implicit alakot ad meg). Érdemes bevezetnünk differenciálegyenletek ezen osztályára egy elnevezést.
Definíció.differenciálegyenlet} Ha a (58)-ben szereplő g és h függvényekhez létezik olyan F=F(x1,x2), mindkét változója szerint kétszer folytonosan deriválható függvény, melyre (60) és (61) egyaránt teljesül, akkor a (58) differenciálegyenletet egzaktnak nevezzük.
Tehát az egzakt (58) differenciálegyenlet megoldásának meghatározását visszavezettük algebrai egyenlet megoldására, azaz a differenciálegyenletet megoldottuk. Ehhez csupán az kellett, hogy ismerjünk egy olyan F függvényt, amely kielégíti (60)-et és (61)-et is. Ezért természetszerűleg merülnek fel a következő kérdések.
- Hogyan tudjuk megállapítani a (58) differenciálegyenletről, hogy egzakt-e vagy sem?
- Ha tudjuk, hogy egzakt, akkor milyen eljárással kaphatunk meg egy megfelelő F-et?
- Ha nem egzakt, akkor hogyan lehet ekvivalens átalakításokkal egzakttá tenni?
Az első két kérdésre az alábbi tétel adja meg a választ, míg az utolsó kérdéssel a következő, 2.5.1 alfejezet foglalkozik.
Tétel. A (58) differenciálegyenlet pontosan akkor egzakt, ha
| |
(52) |
Bizonyítás. Tételezzük fel először, hogy (58) egzakt és legyen F olyan kétszer folytonosan differenciálható függvény, melyre (60) és (61) teljesül.
Mivel F kétszer folytonosan differenciálható, ezért a (Young-tétel szerint) a vegyes másodrendű deriváltak egyenlőek, azaz
| |
(53) |
Továbbá
Most belátjuk: (64) elégséges ahhoz, hogy létezzen F, melyre (60) és (61) teljesül, azaz (58) egzakt. Bizonyításunk alkalmas lesz arra, hogy megfelelő F-et meg is kaphassunk.
A (60) alatti
![]()
| |
(54) |
Hasonlóan, F pontosan akkor elégíti ki (61)-t, ha létezik c2 egyváltozós függvény, amellyel
| |
(55) |
Be kell most bizonyítanunk, hogy (64) fennállta esetén (68) és (69) egyaránt fennáll valamilyen c1-gyel, illetve c2-vel. (Megjegyezzük, hogy konkrét feladatok esetén c1-et és c2-t próbálgatással rendszerint könnyű megtalálni.)
Jelöljük az (64)-ban szereplő, egymással egyenlő deriváltfüggvényeket r=r(x1,x2)-vel. Hasonló meggondolással, mint az előbb, a
![]()
![]()
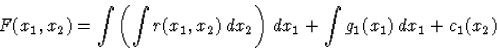 |
(56) |
Hasonlóan, (69) egyenértékű az
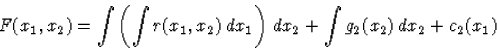 |
(57) |
E két feltétel, (70) és (71) mindegyike fennáll, ha
![]()
Lássunk most néhány példát az előzőek alkalmazására.
5-1. kidolgozott feladat.
Oldjuk meg az
kezdetiérték-feladatot!
Megoldás: A kezdetiérték-feladatnak egyértelmű megoldása létezik, mert a differenciálegyenlet jobb oldalának az (x0,y0)=(1,2) környezetében y szerinti folytonos deriválhatósága miatt teljesíti a Lipschitz-feltételt (v.ö. egzisztencia és unicitási tétel, (1.4) alfejezet).
Átszorozva a differenciálegyenletet a jobb oldal nevezőjével rendezés után a
![]()
Vizsgáljuk meg, hogy az előálló differenciálegyenlet egzakt-e!
Mivel
ezért a parciális deriváltak egyenlősége miatt az egyenlet egzakt.
Keressünk megfelelő F függvényt!
| |
(58) |
| |
(59) |
![]()
F(x,y)=x2y+3x3-y2
függvény felhasználásával a kezdetiérték-feladat megoldásaira azx2y+3x3-y2=k
implicit alakot kapjuk, ahol k alkalmas valós szám. A kezdeti feltételből k-ra 2+3-4=k, azaz k=1 adódik, így a kezdetiérték-feladat megoldása kielégíti azx2y+3x3-y2=1
egyenletet. Ez másodfokú y-ra nézve, amelyet megoldva (csak azt a gyököt tartva meg, amely a kezdeti feltételt is kielégíti) a kezdetiérték-feladat megoldása| |
(60) |
Megjegyezzük, hogy ha nem akarunk a feladat megoldása során az említett
egzisztencia- és unicitási tételre hivatkozni, akkor elegendő az y-ra
(74) alatt kapott formulát visszahelyettesíteni az eredeti differenciálegyenletbe, hogy
meggyőződjünk: valóban kielégíti a differenciálegyenletet.
5-2. kidolgozott feladat.
Igazoljuk, hogy a
![]()
y(0)=2
kezdeti értékhez tartozó megoldását!Megoldás: Mivel
![]()
![]()
Határozzuk meg most F-et!
![]()
![]()
![]()
![]()
![]()
F(x,y)=(4x3+x+1)y+x2+6x,
így a differenciálegyenlet megoldásaira a![]()
A kezdeti feltételt figyelembe véve k=2 adódik, ezért a kezdetiérték-feladat megoldása:
![]()
5-3. kidolgozott feladat.
Oldjuk meg az
kezdetiérték-feladatot!
Megoldás: A differenciálegyenlet egzakt, hiszen a jobb oldalak egkyenlők az alábbi összefüggésekben:
F meghatározásakor az alábbiakat kapjuk.
![]()
továbbá
![]()
![]()
![]()
![]()
![]()
Az y(5)=0 kezdeti feltételt figyelembe véve ![]() .Ezért a kezdetiérték-feladat megoldására az
.Ezért a kezdetiérték-feladat megoldására az
![]()
![]()
![[*]](nyil_elore.gif)
Készült a SZIF-MML-rendszer felhasználásával