![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

Az integráló tényező
Láthattuk, hogy egy egzakt egyenlet megoldásának felírása viszonylag egyszerű. Mit tegyünk akkor, amikor azt tapasztaljuk, hogy a (57)-ból származó (58) egyenlet nem egzakt?
Szorozzuk be (57) mindkét oldalát egy (egyelőre ismeretlen) p=p(x1,x2) függvény felhasználásával p(x,y(x))-szel és próbáljuk p-t úgy megválasztani, hogy az előálló
| |
(61) |
![[*]](foot_motif.gif)
Definíció. Az olyan p függvényt, amelyre (75) egzakt, integráló tényezőnek nevezzük.
Előző tételünket alkalmazva azt kapjuk, hogy (75) pontosan akkor lesz egzakt, ha p kielégíti a
| |
(62) |
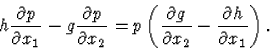 |
(63) |
![[*]](foot_motif.gif) mellett létezik megoldása, de meghatározása rendszerint bonyolultabb,
mint az eredeti (58) megoldása. Ezért azt lehet tenni, hogy
csak függvényeknek egy szűkebb osztályában keressük a parciális differenciálegyenlet egy megoldását, olyan függvényosztályban, amely ha tartalmaz megoldást,
akkor azt kis fáradsággal elő tudjuk állítani.
Persze, a leszűkített függvényosztályban nem feltétlenül lesz
megoldása (77)-nek; ilyenkor más függvények között kell
keresnünk integráló tényezőt.
mellett létezik megoldása, de meghatározása rendszerint bonyolultabb,
mint az eredeti (58) megoldása. Ezért azt lehet tenni, hogy
csak függvényeknek egy szűkebb osztályában keressük a parciális differenciálegyenlet egy megoldását, olyan függvényosztályban, amely ha tartalmaz megoldást,
akkor azt kis fáradsággal elő tudjuk állítani.
Persze, a leszűkített függvényosztályban nem feltétlenül lesz
megoldása (77)-nek; ilyenkor más függvények között kell
keresnünk integráló tényezőt.
Első kísérletképpen próbáljuk p=p(x1,x2)-t azon
kétváltozós függvények között keresni, amelyeknél p nem függ a
második argumentumtól, x2-től, azaz p=p(x1). Ez azért okoz
könnyebséget az integráló tényező kiszámításánál,
mert ilyen p-re a (77) egyenlet csak közönséges differenciálegyenlet (hiszen 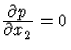 , lévén p független x2-től).
, lévén p független x2-től).
| |
(64) |
![[*]](foot_motif.gif) a megoldandó (77) egyenlet az alábbi alakban írható:
a megoldandó (77) egyenlet az alábbi alakban írható:
![]()
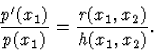 |
(65) |
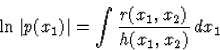
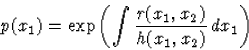 |
(66) |
![[*]](foot_motif.gif) eleget tesz.
eleget tesz.
Így bebizonyítottuk az alábbi tételt.
Tétel. Ahhoz, hogy (58)-nek létezzen csak x1-től függő p integráló tényezője szükséges és elégséges, hogy
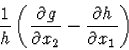 |
(67) |
Amennyiben ez teljesül, úgy egy integráló tényező felírható a (80) alatti alakban, ahol r-et (78) definiálja.
Teljesen ugyanígy kaphatunk feltételt csak x2-től függő integráló tényező létezésére.
Tétel. Ahhoz, hogy (58)-nek létezzen csak x2-től függő p integráló tényezője szükséges és elégséges, hogy
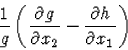 |
(68) |
Amennyiben (82) teljesül, úgy az integráló tényező felírható a
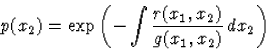 |
(69) |
Felhívjuk a figyelmet a (80) és a (83) egyenletek jobb oldalán szereplő integrandusok azon eltérésére, hogy az utóbbi képlete egy mínusz előjelet tartalmaz. Ez onnan jön be, hogy (83) (80)-ból úgy kapható meg, hogy ez utóbbiban a g és h függvényeket, valamint az x1 és x2 változókat felcseréljük; márpedig ennél a cserénél r éppen (-1)-szeresére változik.
5-4. kidolgozott feladat.
Tekintsük az
differenciálegyenletet.
a) Adjunk meg egy integráló tényezőt (84)-hez!
![]()
(70)
b) Írjuk fel és oldjuk meg az előző pontban kapott integráló tényezőnek megfelelő egzakt differenciálegyenletet!
Megoldás: Az előző tételekben szereplő elnevezéseket használjuk, így
![]()
![]()
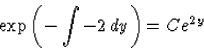
p(y)=e2y
integráló tényezője (84)-nek.b) A p-nek megfelelő egzakt differenciálegyenlet:
| |
(71) |
Látható, hogy
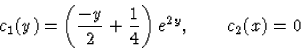
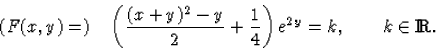
5-5. kidolgozott feladat.
Adjunk meg egy integráló tényezőt az
![]()
Megoldás: Használva az (78) alatti jelölést
![]()
![]()
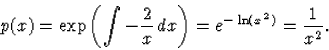
![[*]](nyil_elore.gif)
Készült a SZIF-MML-rendszer felhasználásával