![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)
 |
Itt az alábbi trükk lesz a segítségünkre: szorozzuk be a
differenciálegyenlet mindkét oldalát 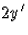 -vel: -vel:
| 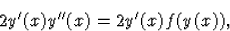 |
(87) |
és vegyük észre, hogy az egyenlet bal oldala éppen 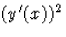 deriváltja. Így (101) az alábbi alakba írható: deriváltja. Így (101) az alábbi alakba írható:
| 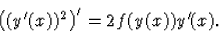 |
(88) |
Integrálva (102) mindkét oldalát, majd a jobb oldalon a
helyettesítéses integrálás képletét alkalmazva:
ahol
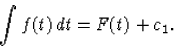
(103) pedig már egy elsőrendű differenciálegyenlet a keresett y függvényre nézve,
és mivel a jobb oldal x-et nem tartalmazza, ezért szétválasztható
változójú.
|
![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

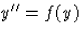 eset
eset
![]() -vel:
-vel:
![]()
![[*]](nyil_elore.gif)
![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

![]()
![[*]](nyil_elore.gif)