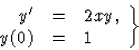A hatványsor-módszer Ennek a módszernek a segítségével a 1.3 alfejezetben kitűzött feladatok közül a kezdetiérték-feladatok megoldására kapunk közelítéseket, annak x0 körüli Taylor-polinomjai (speciális esetekben Taylor-sorának) alakjában. A Taylor-polinomok pedig - amint azt az analízisből tudjuk - elég gyakran jól közelítik a kifejtett függvényt a kifejtési pont, x0 közelében. Tekintsük először az elsőrendű 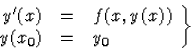  $$\left.\begin{array} {rcl} {y}^\prime(x) &=&f(x,y(x)) \\ y(x_0)&=&y_0 \end{array}\right\}$$ (99) kezdetiérték-feladatot. A módszer lényege az, hogy ha a differenciálegyenlet jobb oldalát deriváljuk x szerint, akkor megkapjuk y deriváltjait, lévén az eredeti differenciálegyenlet bal oldala. Csak az a baj, hogy a deriváltakra előálló formula tartalmazza az ismeretlen y függvényt is, hiszen azt a jobb oldal, f(x,y(x)) is tartalmazza, ezért a deriváltak értéke általában ismeretlen. Azonban y-nak egy pontban, x0-ban ismerjük a helyettesítési értékét: a kezdeti feltétel szerint ez y(x0)=y0; így ebben a pontban ki tudjuk értékelni a deriváltakat. Ezek segítségével felírhatók a keresett Taylor-polinomok. Másodrendű differenciálegyenletekhez tartozó kezdetiérték-feladatoknál a módszer ugyanez, csak az egyenletek deriválásával mindig eggyel magasabb rendű deriváltját kapjuk meg y-nak, mint az előbb. Nézzük meg most pontosabban az előbb mondottakat. Állítás. Ha f n-szer folytonosan deriválható az (x0,y0) pont környezetében, akkor a (116) kezdetiérték-feladat y megoldása n+1-szer deriválható x0-ban és az y(k)(x0), $k=1,\ldots,n+1$ deriváltak kifejezhetők x0, y0 és f parciális deriváltjai (x0,y0) helyen felvett helyettesítési értékeivel. Bizonyítás. Először nézzük meg az állítást n=1-re. A láncszabályt felhasználva deriváljuk a differenciálegyenlet jobb oldalát x szerint! Ez megtehető, mert a feltételezések szerint f és y is differenciálható. (A könnyebb olvashatóság miatt a második egyenlőségjeltől a parciális deriváltakra az indexes jelölésmódot használjuk, továbbá az y függvény x és az f és parciális deriváltjainak (x,y(x)) argumentumait sem írjuk ki.) $$\frac{df(x,y(x)}{dx}=\frac{\partial f}{\partial x}(x,y(x))\cdot1+ \frac{\partial f}{\partial y}(x,y(x)){y}^\prime(x)=f_x+f_yf,$$ kihasználva még azt, hogy y megoldása a differenciálegyenletnek, így ${y}^\prime=f$. Ezért a differenciálegyenlet bal oldala, is deriválható és   $${y}^{\prime\prime}=f_x+f_yf.$$ (100) n=2-re az állítás ugyanígy látható be: (117) jobb oldala x szerint deriválható és a deriválást elvégezve kapjuk: amit átrendezve és -et beírva ${y}^{\prime\prime\prime}$-re az   $${y}^{\prime\prime\prime}=f_{xx}+2f_{xy}f+f_{yy}f^2+f_y(f_x+f_yf)$$ (101) formulát kapjuk. Ez az eljárás láthatóan akármekkora n-re működik. A pontos bizonyítást jelentő n+1-ig terjedő teljes indukciót itt elhagyjuk.   Ezután y deriváltjainak x0 helyen felvett értékeihez úgy jutunk, hogy az (x0,y0) ponton kiszámítjuk (117), (118) és a többi deriváltra vonatkozó egyenletek jobb oldalát. Így eljutunk y n-edfokú Tn Taylor-polinomjához, melynek alakja: 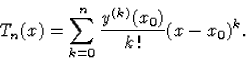  $$T_n(x)=\sum_{k=0}^{n}{\frac{y^{(k)}(x_0)}{k\,!}(x-x_0)^k.}$$ (102) Ez szolgál az y pontos megoldás közelítésére. Mielőtt e közelítés hibájának a becslésére is alkalmazható formulát ismertetnénk, lássunk a módszer alkalmazására egy példát! Hogy legyen összehasonlítási alapunk olyan differenciálegyenletre fogjuk alkalmazni, amelynek a pontos megoldása ismert.   1-1. kidolgozott feladat. Adjuk meg az $$\left.\begin{array} {rcl} {y}^\prime &=&2 x y,\\ y(0)&=&1\end{array}\right\}$$ kezdetiérték-feladat megoldásának x0=0 körüli 4-edrendű Taylor-polinomját! 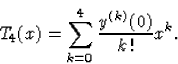Megoldás: A keresett polinom alakja: $$T_4(x)=\sum_{k=0}^{4}{\frac{y^{(k)}(0)}{k\,!}x^k.}$$ A kezdeti feltételből: y(0)(0)=y(0)=1; a differenciálegyenletből: $$y^{(1)}(0)={y}^\prime(0)=2\cdot0\cdot1=0.$$ Deriválva a differenciálegyenletet:   $${y}^{\prime\prime}=2y+2x{y}^\prime=2y+2x\cdot2xy=2y+4x^2y,$$ (103) így $${y}^{\prime\prime}(0)=2\cdot1+4\cdot0\cdot1=2.$$ Hasonlóan   $${y}^{\prime\prime\prime}={(2y+4x^2y)}^\prime=2{y}^\prime+8xy+4x^2{y}^\prime= 4xy+8xy+8x^3y=12xy+8x^3y,$$ (104) ezért $${y}^{\prime\prime\prime}(0)=0;$$ $${y}^{\prime\prime\prime\prime}={(12xy+8x^3y)}^\prime=12y+12x\cdot2xy+24x^2y+8x^3\cdot2xy= 12y+48x^2y+16x^4y,$$ ahonnan $${y}^{\prime\prime\prime}(0)=12.$$ Így $$T_4(x)=1+\frac{0}{1\,!}x+\frac{2}{2\,!}x^2+\frac{0}{3\,!}x^3+\frac{12}{4\,!} x^4=1+x^2+\frac12x^4.$$ Most a pontos megoldást fel tudjuk írni a korábban tanult módszerek segítségével (a differenciálegyenlet szétválasztható változójú (és lineáris is)). A megoldás: y(x)=ex2, amelynek a Taylor-sora (felhasználva ex Taylor-sorát) az alábbi alakban írható fel: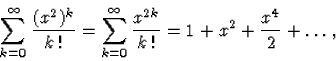 $$\sum_{k=0}^{\infty}{\frac{(x^2)^k}{k\,!}}= \sum_{k=0}^{\infty}\frac{x^{2k}}{k\,!}=1+x^2+\frac{x^4}{2}+\ldots\,,$$ ahonnan láthatjuk, hogy valóban jól számoltunk az előbb.   Egy példa végigszámolása után jól láthatjuk, hogy tulajdonképpen felesleges volt (120)-ben és (121)-ban -nek a differenciálegyenletből származó képlettel való helyettesítése. Ezt az alakot is vihettük volna tovább és amikor ezt a tagot deriválni kell, akkor azt csak formálisan kijelöljük. Amikor a konkrét x0 helyen kell kiszámolni a helyettesítési értékeket, addigra már a megfelelő deriváltak értékei már rendelkezésre fognak állni. A fenti példánál maradva, a (120) és (121) egyenletek helyett elég lett volna az alábbiakat írni. $${y}^{\prime\prime}=2y+2x{y}^\prime,$$ ahonnan - ${y}^\prime(0)=1$-et felhasználva - Hasonlóan $${y}^{\prime\prime\prime}=2{y}^\prime+2{y}^\prime+2x{y}^{\prime\prime},$$ ahonnan - az előbb kiszámított ${y}^{\prime\prime}(0)=0$-t felhasználva - $${y}^{\prime\prime\prime}(0)=2\cdot 1+2\cdot 0+2\cdot 2=6.$$ Ezt az eljárást folytathatnánk végig. Ez a módosítás elég sok számítástól megkímél bennünket, főleg akkor, ha f parciális deriváltjai bonyolultak.      1-2. kidolgozott feladat. Írjuk fel az $$\left.\begin{array} {rcl} x^2{y}^{\prime\prime}+x{y}^\prime-y &=&0,\\ y(1)&=&2,\\ {y}^\prime(1)&=&0\end{array}\right\}$$ kezdetiérték-feladat megoldásának harmadfokú, x=1 körüli Taylor-polinomját! 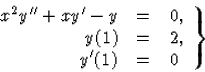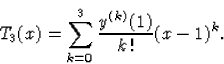Megoldás: A polinom alakja: $$T_3(x)=\sum_{k=0}^3{\frac{y^{(k)}(1)}{k\,!}(x-1)^k}.$$ A szükséges deriváltak közül kettőt ismerünk a kezdeti feltételből: $$y^{(0)}(1)=y(1)=2\qquad\mbox{és}\qquad y^{(1)}(1)={y}^\prime(1)=0.$$ A maradék két együttható számolásához először fejezzük ki -t a differenciálegyenletből:   $${y}^{\prime\prime}=-\frac{{y}^\prime}{x}+\frac{y}{x^2}.$$ (105) Innen közvetlen behelyettesítéssel ${y}^{\prime\prime}(1)=-\frac{0}{1}+\frac{2}{1} =2$ adódik. Deriválva (122)-t: $${y}^{\prime\prime\prime}=-\frac{{y}^{\prime\prime} x-{y}^\prime}{x^2}+\frac{{y}^\prime x^2-2xy}{x^4},$$ ahonnan $${y}^{\prime\prime\prime}(1)=-\frac{2-0}{1}+\frac{0-4}{1}=-6.$$ Így a keresett polinom: T3(x)=2+(x-1)2-(x-1)3. Speciális esetekben az ismertetett hatványsor-módszer megadja a megoldás teljes Taylor-sorát is, nemcsak egy Taylor-polinomját. Akkor lehetséges ez, ha észreveszünk valamilyen, legtöbbször rekurziós formulát az y(k)(x0) értékekre.   1-3. kidolgozott feladat. Adjuk meg az $$\left.\begin{array} {rcl} {y}^\prime &=&5 y,\\ y(0)&=&3\end{array}\right\}$$ kezdetiérték-feladat megoldásának x0=0 körüli Taylor-sorát! 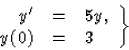Megoldás: Számítsunk ki először néhány deriváltat és próbáljuk megsejteni belőlük az általános formulát! Ezekből azt sejtjük, hogy y(k)=5ky. Ezen állítás bizonyítása k szerinti indukcióval könnyen elvégezhető. Valóban, k=0-ra és k=1-re nyilvánvalóan, k=2,3,4-re az előbb látottak miatt igaz; továbbá ha k-ra igaz, akkor k+1-re: amit igazolni kellett. 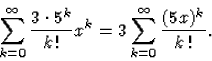Ezért minden k természetes számra $$y^{(k)}(0)=5^ky(0)=3\cdot5^k,$$ így a keresett Taylor-sor: $$\sum_{k=0}^{\infty}{\frac{3\cdot5^k}{k\,!}x^k}= 3\sum_{k=0}^{\infty}{\frac{(5x)^k}{k\,!}}.$$ Ez viszont könnyen észrevehetően éppen 3e5x Taylor-sora, ezért a megoldás y(x)=3e5x. Megjegyezzük, hogy a megoldást megkaphattuk volna pl. a változók szétválasztásának módszerével is.

Dr. Horváth Zoltán:Bevezetés a differenciálegyenletek megoldásábaKészült a SZIF-MML-rendszer felhasználásával